Kvizy
Archiv kvizů, které na našem webu vycházely kdysi v minulém tisíciletí...
ÚLOHA číslo 50: (duben)
Za sedmero horami a sedmero řekami bývalo město, kde si byli manželé nevěrní. Doslechl se o tom král a poslal proto svého posla s krutým příkazem. Každý muž, který zjistí, že je mu žena nevěrná, ji může ještě tu noc zabít. Samozřejmě, že kdejaký muž věděl, která z cizích žen je nevěrná, ale nevěděl to o své manželce. Po vyslechnutí příkazu se každý den, vždy ráno, ráno sešli muži toho města u kašny na náměstí, aby si oznámili, kdo svojí ženu tu noc zabil. Tak se také dozvěděli, že třetí noc zabil svou ženu rychtář... Víte, kolik je ve městě nevěrných žen?
Správnou odpověď zaslal například ing. Jan Kral
Neverne manzelky jsou 3. Protoze kdyby byla jedna, tak je jen jeden z manzelu, ktery nevi o zadne a zabije ji hned prvni noc. Kdyby to byly dve, tak vsichni, az na prislusne manzely znaji 2 a manzele nevernych zen znaji jen jednu cizi, o sve to nevi, ale protoze vi, ze minulou noc nebyla zabita zadna, vedel by ze je parohac. Takze to taky neni ten pripad. Protoze vsak byla zabita manzelka az treti noc, tak jeji manzel vedel o dvou nevernicich a protoze zadna z nich nebyla zabita minulou noc, tak musela by neverna i jeho zena. Kdyby nevernych znal vic, tak by hned treti noc nemohl podezirat tu svou.
ÚLOHA číslo 49: (březen)
Lovec zahlédl medvěda, v tu chvíli byl lovec přesně 100 metrů od něj směrem na jih. Medvěd se ani nehnul. Aby ho medvěd nezavětřil, lovec pomalu postupoval 100 metrů na východ. Medvěd stále seděl na místě, a tak lovec namířil pušku přesně na sever a medvěda trefil. Jakou má medvěd barvu?
Většina s vás správně uhodla, že medvěd má bílou barvu. Je to totiž medvěd lední, protože celá historka se odehrála na severní točně. Medvěd seděl na pólu - pokud se lovec pohnul kterýmkoli směrem a pak střelil na sever, musel medvěda trefit.
ÚLOHA číslo 48: (únor)
Minulý víkend jsem byl se svým malým synovcem lyžovat. Nahoru jsme se vozili na kotvovém vleku. Doba jízdy byla dlouhá a synovec se pořád ptal, zda už budeme nahoře. Všiml jsem si, že v jednom okamžiku měla kotva jedoucí naproti nám číslo 95 a že následující kotva měla číslo 0. Podíval jsem se tedy na číslo naší kotvy, bylo to 66. Mohl jsem tedy synovci říci, že už tam budeme, že už jsme za polovinou ? (Dětem se nemá lhát)
Správnou odpověď na únorový kviz poslal například pan František Zelina.
Ne, ještě nejsme. Nahoře je 66 kotev (0 až 66), dole je 29 kotev (66 až 95) - ještě nejsme v polovině.
ÚLOHA číslo 47: (leden)
Pepíček, známý darebák, si nabral v cukrárně pytlík bonbonů. Protože prodavač na něj chtěl výchovně zapůsobit, položil mu následující otázku: "Když mi o těch bonbonech řekneš pravdu, prodám ti je za 20 Kč. Když ale řekneš lež, prodám ti je za plnou cenu, za 50 Kč." Co Pepíček řekl, že prodavač pak nevěděl, za jakou cenu mu má bonbony prodat, a tak si je Pepíček odnesl zadarmo ?
Jedno z možných správných řešení poslal například pan Pavel Janoušek.
Pepíček řekne prodavači: "Bonbony mi prodáte za 50 Kč". Kdyby mu je prodavač prodal za 50 Kč, řekl by Pepíček pravdu a musel by je dostat za 20 Kč. Kdyby mu je prodavač prodal za jakoukoliv jinou cenu než 50 Kč, řekl by Pepíček lež a prodavač by mu je musel prodat za 50 Kč. Pro prodavače nemá úloha řešení, proto je dal Pepíčkovi zadarmo.
ÚLOHA číslo 46: (prosinec)
Předevčírem bylo Zuzance devět let. Příští rok jí bude dvanáct. Jak je to možné ?
Správné řešení poslal například pan Pavel Valášek:
Zuzanka se narodila 31.12.1993, dnes je 1.1.2004, takže předevčírem měla 9, včera už 10, letos na Silvestra oslaví 11 - no a příští rok (na Silvestra 2005) bude mít 12.
ÚLOHA číslo 45: (listopad)
Při uklízení jsem zjistil, že kávová lžička a hrnek na kávu váží dohromady stejně jako hrnek na čaj. Pět kávových lžiček zase váží stejně jako hrnek na čaj a hrnek na kávu dohromady. Kolik hrnků na kávu váží dohromady stejně jako hrnek na čaj s kávovou lžičkou ?
Správné řešení poslal například pan Tomáš Humpolec:
Označíme K = hrnek na kávu, L = lžička a C = hrnek na čaj.
Pak tedy ze zadání platí L + K=C a 5L = C + K, máme zjistit xK = C + L. Po zkrácení C = 1,5K a L = 0,5K tedy 2K = C + L, správná odpověď tedy je: DVA hrnky na kávu váží stejně jako lžička a hrnek na čaj.
ÚLOHA číslo 44: (říjen)
V závodě na 400 m porazil Franta Marii v cíli o 80 m. Dohodli se, že v opakovaném závodě bude Franta startovat o 100 m za startovní čarou. Je to tak správné, jestliže mají být šance vyrovnané ? (Předpokládáme, že oba běhají konstantní rychlostí.)
Správné řešení poslal například pan Oldřich Ohryzek:
Ano, šance budou vyrovnané. Platí v = s/t. Pokud oba běží konstantní rychlostí, je konstantní i poměr jejich rychlostí a tudíž i poměr dráhy, kterou za stejný čas uběhnou (v tomto případě 320/400 = 400/500).
ÚLOHA číslo 43: (září)
Princezna je uvězněna v zámku se čtvercovým půdorysem, okolo něj je čtvercový příkop, všude 10m široký. Honza, který jde princeznu zachránit před drakem, právě dorazil k příkopu a přemýšlí, jak se dostat na druhou stranu. Nalezl sice 2 prkna, ale jsou dlouhá jen 9,5 m. Jak to provede ? (Prkna nemá čím spojit, plavat neumí a je hodně těžký, protože jí moc buchet - když zkusil vstoupit na metr přečnívající prkno, hned jak udělal krok, málem spadl do vody.)
Správné řešení poslal například pan František Zelina:
V libovolném rohu položí 1 prkno napříč tak, že oba konce leží na 2 kolmých stranách břehu. Po tomto prknu přejde do jeho středu a zde 2. prknem spojí střed 1. prkna s protějším břehem (tato vzdálenost je menší než 9,5m).
ÚLOHA číslo 42: (srpen)
Je dán čtverec. Rozdělte jej přímkami na 13 stejných dílů (úlohu poslal ing. Vítězslav Čapek).
Řešení je velmi jednoduché, správnou odpověď poslal například pan Miroslav Beneš:
Nejjednoduššší je rozdělělit čtverec 12 rovnoběžnými přímkami tak, aby mezi nimi navzájem a mezi krajními přímkami a stranami čtverce byla vzdálenost 1/13 strany čtverce. Tímto bude čtverec rozdělen na 13 stejných obdélníků.
ÚLOHA číslo 41: (červenec)
Jana má klece s papoušky. Žádná klec není prázdná. Platí také, že Jana má více klecí, než papoušků v kterékoliv kleci. Mohou být za těchto podmínek papouškové rozmístěni tak, aby v žádné kleci nebyl stjený počet papoušků ?
Správnou odpověď poslal například pan ing. Zdeněk Jahoda:
Papoušky není možno za daných podmínek rozmístit. V aritmetické řadě s d=1 (různý počet papoušků v jednotlivých klecích) a a1=1 (žádná klec prázdná) je vždy an=n (an je počet papoušků v kleci n). Při vyšším počtu klecí, než je maximální počet ptáků v kterékoliv kleci by musela být proto jedna klec prázdná nebo alespoň ve dvou z nich by musel být počet papoušků shodný.
ÚLOHA číslo 40: (červen)
Mám 2 skleničky, v jedné je bílé víno, ve druhé červené. Skleničky nejsou plné. Přeliji jednu lžičku bílého vína do červeného, zamíchám a pak přeliji lžičku této směsi do bílého. Nic nepřeteklo, obou vín bylo na začátku i po skončení stejně. Která odpověď popisuje správně stav po skončení experimentu:
a) Bílého vína je více v červeném než červeného v bílém.
b) Červeného vína je více v bílém než bílého v červeném.
c) Bílého vína je v červeném stejně jako červeného v bílém.
Správná odpověď je c), ale protože červnový kvíz byl chyták, uveďme 2 řešení:>
Řešení výpočtem - od pana Pavla Štětiny:
Řekněme, že na počátku mám 20/20 (B) bílého vína a 20/20 (Č)červeného. Když přeliju 5/20 B do Č, dostanu mix s obsahem 5/25 B a 20/25 Č. Z tohoto mixu vezmu opět dílek o velikosti 5, který ovšem obsahuje 1:4 B:Č. Ve sklenici Č nyní zbývá 4:16 B:Č a ve sklenici B dostanu 16:4 B:Č.
Řešení úvahou - od pana Evžena Horny:
Pokud je v obou sklenicích, na začátku i na konci, stejně, to co v jedné chybí, musí být doplněno stejným množstvím z druhé. Poměry jsou tedy zcela opačné a bílého v červeném je stejně jako červeného v bílém.
ÚLOHA číslo 39: (květen)
Byl máj a Lenka a Tomáš se spolu scházeli. Napřed se vždy šli projít, a pak si v místní vinárně dlouho povídali při svíčkách. Přitom si všimli zajímavé věci: Ve vinárně jim vždy zapálili dvě svíčky rozdílné výšky i objemu. Ta vyšší pokaždé vyhořela za tři a půl hodiny a ta menší za pět hodin. Po dvou hodinách hoření byly obě stejně vysoké.
Věděli byste, v jakém poměru jsou jejich výšky před zapálením ?
Správné řešení poslal například pan ing. Jahoda:
Pokud označíme výšky nezapálených svíček a resp. b, odhoří za 1 hodinu a/3,5, resp. b/5. Po dvou hodinách hoření jsou proto jejich zbytky a*1,5/3,5 resp. b*3/5, které jsou dle zadání shodné. Po této úvaze je pak jednoduché spočítat poměr jejich počátečních délek: a/b = 3/5 * 3,5/1,5 = 1,4 (celočíselně 5:7).
ÚLOHA číslo 38: (duben)
Amatérské fotbalové mužstvo lidových vyprávěčů odjíždělo k důležitému utkání a v autobuse se nemluvilo o ničem jiném, než jak zápas dopadne. Když se vraceli domů, zjistili, že pouze jeden z nich tipoval správně. Přijdete na to, kdo z nich to byl a jakého bylo dosaženo výsledku? Zde jsou jejich předpovědi:
Česal: Vyhrajeme nejméně o 3 branky.
Dohnal: Nedáme ani gól.
Hejzák: Vyhrajeme 2:1.
Jelínek: Celkem padne nejméně 5 branek.
Karas: Dáme pouze jednu branku.
Los: Nedostaneme ani jednu branku.
Novák: Dáme 2 góly.
Pithart: Prohrajeme nejméně o 2 branky.
Rikl: Dáme více než dvě branky.
Strop: Jeden ze soupeřů zvítezí o jednu branku.
Železný: Dostaneme pouze jednu branku.
Správné řešení poslal například pan Jiří Osoba:
Prozkoumáním všech výsledků do stavu 4:4 (pak už vždy platí "Celkem padne nejméně 5 branek" a zároveň jedna z podminek "Dáme více než dvě branky" nebo "Prohrajeme nejméně o dvě branky") jsem dospěl k výsledku 2:2 a pravdu měl Novák (Dáme 2 branky).
ÚLOHA číslo 37: (březen)
Na polích blízko sebe pracovali dva sedláci, Vojtěch a Josef. Za sedlákem Vojtou přišel v poledne syn Jiří, za sedlákem Josefem dcera Marie. Jiří byl 2x starší než Marie. Další den přišla Marie se svou sestrou Janou, součet věků obou děvčat byl dvakrát vyšší než stáří Jiřího. Následující den přivedl Jiří svého bratra Tomáše a tím byl součet věků obou chlapců dvakrát větší než součet věků obou děvčat. Dívky přivedly příští den svou třetí sestru Aničku a opět součet věků tří děvčat byl 2x větší než součet věků obou chlapců. Otázka zní: určete věk Jiřího, za předpokladu, že Aničce bylo 21 let den před tím, než šla za otcem.
Správné řešení poslal například pan František Zelina:
Pokud uvažujeme větu, že "Aničce bylo 21 let den před tím, než šla za otcem", dostaneme následující:
Jiri = 4
Jiri = 2x Marie
Marie = Jiri/2 = 4/2 = 2
Marie+Jana = Jiří x 2
Jana= (4 x 2) - Marie = 8 - 2 = 6
Jiri + Tomas = (Marie+Jana) x2
Tomas = ((2 + 6)x2) - 4 = 12
Následující den slaví Marie+Jana+Anicka narozeniny a tedy jim věk stoupne o 1:
Marie = 3, Jana = 7, Anicka = 22
(Jiri + Tomas) x2 = Marie+Jana+Anicka
Anicka = ( (4 + 12) x2)- 3 -7 = 32 - 10 = 22
ÚLOHA číslo 36: (únor)
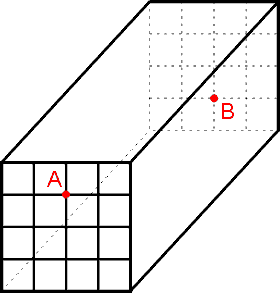
Na obrázku je plný pravoúhlý hranol o rozměrech 4x4x12m. Pro orientaci je na jeho stěnách nakreslena čtvercová síť s rozpětím 1m. Existuje cesta z místa A do místa B, vedená po povrchu hranolu, kratší než 16m? Pokud ano, jaká ?
Správné řešení březnového kvizu poslal například pan ing. Milan Kučera:
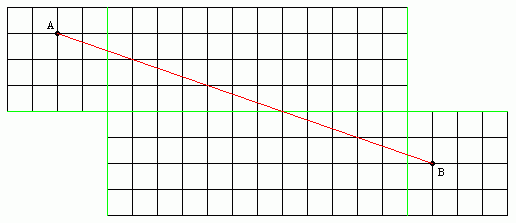
V ortogonálním nezakřiveném světě je nejkratší spojnicí dvou bodů přímka. Nezbývá tedy nic jiného než hledat tu a to nejlépe na rozvinutém plášti. Je to přepona pravoúhlého tojúhelníku o stranách 15 (2+12+1) a 5 (3+2) metrů. Přepona má (dle Pythagorovy věty) jen 15.81m. Plášť (zajímavý fragment) je zobrazen na obrázku.
ÚLOHA číslo 35: (leden)
Pomocí čtyř čtyřek napište všechna čísla od 0 do 10. Můžete použít tyto matematické operace: sčítání, odčítání, násobení a dělení. Je dovolené použít i závorky.
Správné řešení poslala například paní Lucie Vomelová:
44-44=0
44:44=1
(4*4):(4+4)=2
(4+4+4):4=3
(4-4):4+4=4
(4*4)+4:4=5
(4+4):4+4=6
(44:4)-4=7
(4:4)*4+4=8
(4:4)+4+4=9
(44-4):4=10
ÚLOHA číslo 34: (prosinec)
Kdysi dávno za starých dobrých časů se jednoho krásného dne konalo rytířské klání o princezninu ruku. Vítězem se měl stát ten, jehož kůň bude nejpomalejší. Závody byly dlouhé a únavné, ale nakonec přece jen zůstali ti dva úplně nejpomalejší, mezi kterými se mělo rozhodnout. Soupeři nasedli na koně a závod začal. Když už pomalým krokem cestovali asi hodinu, slezli oba s koně a o čemsi nějakou dobu mluvili. Potom zase nasedli na koně a k překvapení všech co nejrychleji uháněli k cíli. Nikdo nechápal, co se děje. O čem si popovídali a co udělali ?
Úlohu přinesl náš kolega Tomáš Jantač.
Správné řešení kvizu zaslal například pan ing. Lukáš Bednář:
Každý nasedl na koně soupeře. Takže pak se musel snažit, aby dojel do cíle co nejdříve, protože tím zajistil, že jeho kůň (na kterém momentálně jel jeho soupeř) byl pomalejší a tím tento zvláštní závod vyhrál. Zároveň tím docílili rychlého průběhu závodu.
ÚLOHA číslo 33: (listopad)
Máte dva doutnáky a funkční zapalovač. Každý z doutnáků hoří přesně 60 minut.
Doutnáky nehoří stejně rychle po celé jejich délce. To znamená, že první polovina jednoho doutnáku může hořet třeba 50 minut. Druhá polovina může hořet zbývajících 10 minut. Druhý doutnák může hořet zase úplně jinak.
Vaším úkolem je odměřit pomocí doutnáků a zapalovače přesně 45 minut.
Pozn.: Doutnák je sňůra, která se zapálí a sama po celé délce vyhoří. Používá se třeba k zapalování výbušnin.
Správné řešení listopadového kvizu zaslal například pan Štěpán Pindur:
45 minut pomocí dvou doutnáků ve vašem příkladě odměříme následujícím způsobem: Jeden doutnák zapálíme na obou koncích a druhý pouze na jednom konci. Po dohoření doutnáku, který jsme zapálili na obou koncích, zapalíme druhý konec druhého doutnáku. Po dohoření druhého doutnáku máme odměřených 45 minut.
Vysvětlení:
První doutnák bude hořet pouze půl hodiny, protože byl zapálen na obou koncích (60 / 2 = 30) (kdyby hořel po celé délce stejně rychle, tak by stačilo pouze ho přepůlit). Tímto způsobem jsme z druhého doutnáku odměřili již zmiňovanou půlhodinu a tím zapálením na jeho druhém konci zbývající čas hoření zkrátíme na polovinu (30 / 2 = 15). A to je dohromady 30 + 15 = 45.
ÚLOHA číslo 32: (říjen)
Trezor, ve kterém je ukryt multimetr, má elektronický zámek. Funguje tak, že po stisku odemykacího tlačítka se na displeji rozsvítí číslo, a ten, kdo chce vstoupit, musí na klávesnici namačkat odpovídající kód utvořený ze zobrazeného čísla. Pokud je kód správný, trezor se otevře.
Známe několik dotazů a správných kódů:
| Displej trezoru | Kód |
| 5 | 5 |
| 15 | 7 |
| 25 | 10 |
| 35 | 10 |
| 45 | 8 |
Jaké číslo na klávesnici navolíte, když na displeji trezoru svítí 55?
Úlohu poslal pan František Zelina.
Říjnový kviz byl vemi těžký. Správné řešení zaslali například pánové Roman Stroblík a Vítězslav Hanák:
Řešení kvízu na téma multimetr v trezoru je 10.
Postup řešení: Trezor ma segmentový display. Uživatel je poučen, jak takový display funguje. Když se mu rozsvítí nějaké číslo, spočítá si počet svítících segmentů dvojčíslí, ten zadá na klávesnici a trezor se mu otevře.
ÚLOHA číslo 31: (září)
Dívám se na čísi podobiznu. Prozradím vám, že nemám sourozence a že otec toho muže na obrázku je syn mého otce. Kdo je na obrázku?
Správnou odpověď zaslal například Jiří Foldyna:
Synem mého otce jsem jen já (nemám sourozence), otec muže na obrázku jsem tedy já, na obrázku je tedy můj syn.
ÚLOHA číslo 30: (srpen)
Dvě mince dávají dohromady 3 Kč, i když jedna z nich není koruna. Co je to za mince?
Srpnový kvíz byl chyták. Správnou odpověď zaslal například pan Aleš Prýmek:
Jedna z nich není koruna (to je dvoukoruna), ale druhá to být může. Takže je to koruna a dvoukoruna.
ÚLOHA číslo 29: (červenec)
Pan Dobřesedal se šel vykoupat k rybníku, ale neznal dobře cestu. Přišel na rozcestí a tam stáli dva bratři. Jeden říká vždy pravdu, druhý jenom lež. Oba odpovídají pouze "ano" nebo "ne". Pan Dobřesedal zjistil jedinou otázkou, která cesta vede k rybníku. Jak to udělal?
Správnou odpověď poslal například pan Miroslav Műller:
Jednoho z bratrů se zaptám: "Souhlasil by váš bratr s tím, že první cesta vede k rybníku?". Pokud odpoví "NE", potom k rybníku vede první cesta, v opačném případě tam vede cesta druhá.
Odůvodnění:
1. První cesta vede k rybníku: Pokud se zeptám bratra, který lže, odpoví "NE", protože jeho bratr by odpověděl "ANO". Pokud se zeptám bratra, který mluví pravdu, potom odpoví "NE", protože i jeho bratr by odpověděl "NE".
2. Druhá cesta vede k rybníku: Pokud se zeptám bratra, který lže, odpoví "ANO", protože jeho bratr by odpověděl "NE". Pokud se zeptám bratra, který mluví pravdu, potom odpoví "ANO", protože i jeho bratr by odpověděl "ANO".
ÚLOHA číslo 28: (červen)
Pyramidou z koulí rozumíme útvar, kdy na plochu položíme do uvažovaného tvaru (zde trojúhelník nebo čtverec) první vrstvu, a pak do vzniklých důlků pokládáme další koule, až v poslední vrstvě je jedna koule na vrcholu. Nejmenší pyramida s trojúhelníkovou základnou je tedy ze 4 koulí, nejmenší pyramida se čtvercovou základnou má 5 koulí. Jednu kouli samotnou nepokládáme za pyramidu. Existuje nějaký počet koulí, z něhož by bylo možno sestavit celou pyramidu i s trojúhelníkovou i se čtvercovou základnou, a přitom by ani v jednom případě žádná koule nezbyla?
Úlohu přinesl náš kolega Tomáš Jantač.
Řešení minulého kvizu není známo.
Z odpovědí vybíráme email od ing. Petr Lupínka:
Takovy počet neexistuje.
Pro další úvahy je N rovno počtu pater.
U pyramidy s trojúhelníkovou základnou platí, že počet koulí daného patra N je roven součtu koulí předchozích (N-1) pater zvětšený o číslo patra, tedy o N.
Dostáváme tedy pro N jdoucí k nekonečnu nekonečnou řadu s konkrétními členy 1, 3, 6, 10, 15, ... což jsou počty koulí jednotlivých pater N.
Matematicky vyjádřeno po úpravě (N2 + N) / 2, celkový počet koulí je součet této řady.
U pyramidy se čtvercovou základnou platí jiný vztah, kdy počet koulí patra N je roven druhé mocnině N.
Dostáváme tedy pro N jdoucí k nekonečnu nekonečnou řadu s konkrétními členy 1, 4, 9, 16, 25, ... což jsou počty koulí jednotlivých pater N.
Matematicky vyjádřeno N2, celkový počet koulí je součet této řady.
Zbývá najít takové N, které je řešením rovnice suma {pro I=1 až N (I2 + I) / 2} = suma {pro I=1 až N (I2)}.
Někdo by to řešil rozkladem řady, já jsem pro ověření použil Excel (skrytá reklama ...) a ověřil si, že do N=3000 nelze nalézt shodu.
Nebyla tedy prohledána celá nekonečná řada, ale jako náznak řešení to snad stačí.
ÚLOHA číslo 27: (květen)
Dva loupežníci uloupili 5 cenných prstenů. Prsteny mají hodnoty všechny navzájem různé. Jak mají loupežníci postupovat, pokud si i při svých loupežnických povahách chtějí lup rozdělit co nejspravedlivěji a záleží jim jenom na získaných hodnotách, ne na počtu prstenů?
Úlohu přinesl náš kolega Tomáš Jantač.
Řešení květnového kvizu:
a) Řesení klasické
- poslal pan Miroslav Beneš (podle nás je toto řešení, které měl autor úlohy na mysli) "bratrským dělením". Jeden z nich (kvůli spravedlnosti se bude losovat) rozdělí prsteny na dvě hromádky. Druhý si jednu z nich vybere, prvnímu připadne zbytek.
b) Řešení matematické:
- poslal pan Martin Poupě: seřadím prsteny do fronty podle jejich hodnoty. Postupně odebírám prsteny z fronty (odebírám z dražšího konce) a vždy dám prsten tomu loupežníkovi, kdo zatím dostal méně; v případě rovnosti (např. hned na začátku) volím náhodně.
c) Řešení prodejní:
- loupežníci prsteny prodají a peníze si rozdělí napůl.
Všechny odpovědi, které byly variantami uvedených, jsme zařadili do slosování.
ÚLOHA číslo 26: (duben)
Potkají se dva kamarádi a první se ptá druhého, kolik má dětí a jak jsou staré. Druhý povídá: "Mám tři syny, součin jejich věku je 36. A součet věku je stejný jako .... jako je tamhle naproti oken." Prvni spočítá okna a pak povídá: "No jo, ale to mi nestačí." Druhý doplní: "Nejstarší syn nosí brýle".
Jaký je věk tří synů a kolik je naproti oken?
Úlohu zaslal pan Václav Derfler, za což mu děkujeme.
Řešení poslal pan Zdeněk Syrovátka:
Věk synu je 2, 2 a 9 let, oken je tedy 13.
Možné výsledky jsou:
1+1+36=38
1+2+18=21
1+3+12=16
1+4+9=14
1+6+6=13
2+2+9=13
2+3+6=11
3+3+4=10
Protože součet věku k vyřešení nestačil, bude se jednat o případ, kdy je součet 13. To je jediný součet, který se vyskytuje více než jedenkrát. A protože nejstarší syn je zřejmě jen jeden (nosí brýle), nebude řešením kombinace 1-6-6, ale 2-2-9.
ÚLOHA číslo 25: (březen)
V místnosti A jsou 3 páčkové vypínače, v místnosti B jsou 3 žárovky bez krytu, každý vypínač ovládá právě jednu žárovku. U každého vypínače je zřejmé, zda je vypnutý, nebo zapnutý. Místnost B je zavřená, není do ní vidět. Vypínače můžete libovolně vypínat a zapínat, pak můžete vstoupit do místnosti B a už s vypínači manipulovat nesmíte. Určete postup, jak v místnosti B rozhodnete, která žárovka patří ke kterému vypínači.
Řešení poslal ing. Martin Poupě
1. Zapnu spínače 1 a 2, 3 nechám vypnutý
2. chvíli počkám (10 minut)
3. Vypnu spínač 2 a jdu do místnosti B
Řešení:
svítící žárovka je ovládána spínačem 1
horká nesvítící žárovka spínačem 2
chladná nesvítící žárovka spínačem 3
ÚLOHA číslo 24: (únor)
Prodavačka v tržnici prodává melouny. První kupec si koupí polovinu melounů a ještě půl melounu. Druhý kupec si koupí opět polovinu zbylých melounů a půl melounu. Třetí nakupující si opět koupí půlku zbytku a půl melounu. Prodavačka je ráda, prodala všechno a žádný meloun nemusela krájet, všechny prodala vcelku. Kolik měla na začátku melounů ?
Řešení zaslal pan Daniel Maxa:
Začněme od konce:
Třetí zákaznik si koupil půlku zbytku a půl melounu (tedy druhou půlku zbytku), dohromady jeden meloun.
Druhý si koupil půl melounu a první půlku původního zbytku, tedy 1/2 a 1, dohromady 2 (než přisel, byly tam tedy 3).
První koupil půl a první půlku původního množství, tedy 1/2 a 3 a 1/2, to je 4.
Na začátku tedy bylo 3 a 4 = 7 melounů.
ÚLOHA číslo 23: (leden)
Na stole leží tři zavřené krabice. Každá krabice má víko, které označuje obsah krabice. JJ - krabice se dvěma jablky, HH - krabice se dvěma hruškami, JH - krabice s jedním jablkem a jednou hruškou. Nepořádný majitel víka zpřeházel tak, že ani jedno není na správné krabici.
Popište, jak lze určit obsah všech krabic po vytažení jednoho kusu ovoce z jedné krabice?
Úlohu přinesl náš programátor Otakar Malý.
Řešení i s důkazem zaslal pan Stanislav Hutar:
Vytáhnu 1 kus z krabice označené jako JH.
Pokud je vytažený kus H, tato krabice obsahuje HH, krabice označená jako JJ obsahuje JH a krabice označená jako HH obsahuje JJ.
Pokud je vytažený kus J, tato krabice obsahuje JJ, krabice označená jako JJ obsahuje HH a krabice označená jako HH obsahuje JH.
Důkaz:
Jsou celkem možne 3 kombinace rozmístění ovoce v krabicích:
označení krabice:
JJ JH HH
obsah:
1. JJ JH HH
2. JH HH JJ
3. HH JJ JH
Kombinace č.1 je zadáním vyloučena - obsah žádné z krabic se neshoduje s jejím označením.
Krabice JH pak ve zbývajících 2 kombinacích obsahuje vždy dvojici shodných kusů ovoce, výběrem jednoho kusu známe i druh druhého a tím i celou kombinaci a tedy obsah zbývajícíh dvou krabic.
ÚLOHA číslo 22: (prosinec)
Závozník přijel na celnici pro zboží. Popletlo se označení beden, ve skladu jich je celkem 5. Závozník ví, že když seřadí bedny podle váhy, tak jeho je ta prostřední. K dispozici má rovnoramenné váhy, může tedy bedny jen porovnávat. Na každou stranu váhy se vejde pouze jedna bedna.
Jak závozník najde správnou bednu na 7 vážení?
Úlohu přinesl ze školy náš programátor Otakar Malý.
Správné řešení zaslal pan ing. Lukáš Bednář:
Bedny si označím: A, B, C, D, E
- Vyberu si jakékoliv tři bedny - první skupinu - (např. A, B, C) a pomocí maximálně tří vážení (A-B, B-C, C-A) je seřadím od nejlehčí k nejtěžší. Dostanu posloupnost např. A<B<C.
Maximálně 3 vážení. - Z výsledné řady první skupiny vyberu prostřední bednu (v našem případě B) a k ní přidám dvě zbývající (D, E) a opět maximálně na tři vážení
(B-D, D-E, E-B)
je seřadím od nějlehčí k nejtěžší.
Maximálně 3 vážení. - Pak:
- jestliže prostřední bedna z první skupiny (zde B) je opět uprostřed řady (tedy např.D<B<E), je tato bedna celkové prostřední.
- jestliže je tato bedna nejlehčí (např. B<D<E), vezmu prostřední z této skupiny (tedy zde D) a zvážím ji s nejtěžší z první skupiny (C). Pak bedna, která je lehčí, je celkově prostřední (tedy např. je-li D<C, pak D je celkově prostřední).
- jestliže je tato bedna nejtěžší (např. D<E<B), vezmu prosřední z této skupiny (tedy zde E) a zvážím ji s nejlehčí z první skupiny (A). Pak bedna, která je těžší, je celkově prostřední (tedy např. je-li A<E, pak E je celkově prostřední).
Celkem maximálně 7 vážení.
ÚLOHA číslo 21: (listopad)
Hloupý Honza má za odměnu dostat místo princezny pytel zlaťáků. Ale král je lakomý a chce mu to ztížit. Proto nechal zlato přetavit do tvaru válce. A aby to měl ještě těžší, nechal odlít druhý, zdánlivě stejný válec z mosazi. Oba válce jsou stejně těžké a mají stejné rozměry (uprostřed zlatého je uzavřená dutina, která ale není vidět).
Jak si má Honza vybrat, aby pak nelitoval ?
Úlohu poslal pan Miroslav Beneš
Jedno z možných řešení zaslal pan František Zelina (přišla i správná řešení, využívající chemickou reakci kovů):
Honza položí oba válce na rovnou podlahu vedle sebe, oba je roztlačí stejnou rychlostí a nechá je kutálet. Vybere si ten, který "ujede" delší dráhu. Zlatý válec má totiž středovou dutinu a tedy větší hmotnost materiálu u obvodu. Proto má větší setrvačnost a bude se kutálet dál než mosazný válec.
ÚLOHA číslo 20: (říjen)
Matka je o 21 let starší než její dítě. Za 6 let bude 5x starší.
Co dělá jeho tatínek?
Úlohu poslal náš bývalý kolega Tomáš Franke.
Z velkého množství správných řešení vybíráme to, které poslal například pan Pavel Surý:
Označme věk dítěte D a věk matky M. Ze zadání sestavíme následující rovnice:
d+21=M
M+6=5*(D+6)
Po úpravě dostaneme
M-D=21
M-5*D=24,
což je "nehomogenní soustava dvou lineárních rovnic o dvou neznámých s regulární maticí a tedy právě jedním netriviálním řešením":
D=-3/4,
M=81/4
Převedeno na roky: D = -9 měsíců , M = 20 let 3 měsíce.
To tedy znamená že budoucí otec si teď někde se svou dvacetiletou přítelkyní pořádně užívají vitaminu S.
ÚLOHA číslo 19: (září 2001)
Máme 10 sloupečků mincí. V každém sloupečku je 10 mincí, z nichž každá váží 10 gramů. Jeden ze sloupečků ovšem obsahuje samé falešné mince, které váží pouhých 9 gramů. K dispozici máme poštovní váhy (s displejem) a s mincemi můžeme volně manipulovat. Jak zjistíme, který sloupeček obsahuje falešné mince, máme-li pouze jedno vážení?
Úlohu přinesl náš programátor Tomáš Jantač.
Dorazilo mnoho názorně popsaných řešení, vybíráme od pana Stanislav Jurnečky:
Z prvního sloupečku dáme na váhu jednu minci, z druhého dvě, z třetího tři, a tak dále až z desátého všech deset mincí. Mince na váze zvážíme. Z výsledné váhy je jasné, kolik falešných devítigramových mincí je na váze a dle toho i ve kterém sloupečku falešné mince jsou. Za předpokladu, že všude by byly mince pravé, byla by výsledná váha 550g. Pokud bude výsledná váha 549g, je na váze jedna falešná mince a tudíž falešné mince jsou v prvním sloupečku. Bude-li váha 548g, jsou na váze dvě falešné mince, které pocházejí ze sloupečku druhého, a tak porad dale, až pokud bude váha 540g, je na váze všech deset falešsných mincí z desátého sloupečku.
ÚLOHA číslo 18: (srpen 2001)
Máme 3 pokusné osoby (Adam, Bohuš, Cyril) a 5 čepic (3 bílé a 2 červené). Osoby sedí za sebou tak, že Adam vidí Bohuše i Cyrila, Bohuš vidí Cyrila a Cyril nevidí nikoho. Každé osobě dáme na hlavu čepici tak, aby ji dotyčný neviděl. každému z nich položíme stejnou otázku:
"Jakou čepici máš na hlavě?"
Adam: "Nevím"
Bohuš: "Nevím"
Otázka: Co odpoví Cyril? Předpokládejte, že všichni 3 uvažují logicky.
Úlohu poslal pan Miroslav Beneš, za což mu děkujeme.
Řešení pěkně popsal pan Martin Locker:
1. Adam říká, že neví. Věděl by jakou má čepici pouze v případě, že Bohuš a Cyril mají červenou. Pak by na něho zbyla bílá. Proto mají Bohuš a Cyril oba bílou nebo jeden bílou a druhý červenou.
2. Bohuš říká, že neví. Ale podle odpovědi Adama ví, že Cyril a on sám nemají oba červenou. Pokud by měl Cyril červenou, musel by Bohuš odpovědět, žemá bílou. Protože neví, tak to znamená, že Cyril má na hlavě bílou.
ÚLOHA číslo 17: (červenec 2001)
Cyril bydlí v Praze na Malé Straně. Má dvě přítelkyně, Alenu a Boženu. Alena bydlí v Hostivaři na konečné tramvaje č. 22, Božena bydlí na Bílé Hoře, kde je druhá konečná linky č. 22. Každou neděli Cyril jednu z nich navštíví. Protože má rád překvapení, přijde na Malostranské náměstí, kudy linka 22 jezdí a nastoupí do tramvaje č. 22 v tom směru, která přijede dřve. Domníval se, že je to spravedlivé řešení, ale když si udělal roční statitstiku, zjistil, že mnohem častěji navštěvuje Alenu než Boženu. Jak je to možné?
Úlohu poslal pan Josef Hanzal, M. S.
Úloha mate zdánlivou symetrií, i programátoři v naší firmě, u kterých se dá předpokládat logické myšlení, dost dlouho uvažovali. Řešení pěkně popsal pan Pavel Chromý:
Předpokládejme, že tramvaje přijíždějí ve stejném intervalu. Vytvořme si tedy posloupnost událostí, sestávající z příjezdu tramvají v jednom (A) a druhém (B) směru. Časová osa bude vypadat asi takto:
> ==A=====B==A=====B==A=====B==>
Pravděpodobnost odjezdu ve směru A je rovna poměru časového úseku od odjezdu B do příjezdu A k délce periody ( = interval tramvaje). Obdobně pro druhý směr. Je zřejmé, že i když jsou intervaly stejné, časové úseky A-B a B-A mohou být různé.
ÚLOHA číslo 16: (červen 2001)
Máme 9 kuliček, vzhledově jsou stejné. Přesto je jedna z nich lehčí nebo těžší. Dále máme dvouramenné váhy bez závaží, kterými můžeme pouze porovnávat, zda jsou předměty na jedné misce těžší (nebo váží stejně) než na druhé. Dokážete určit pouze třemi váženími, která kulička je odlišná a zda je lehčí nebo těžší?
Úlohu přinesl kolega Pavel Furbach
Řešení pěkně popsal pan Dan Maxa:
Kuličky rozdělíme na 3 skupiny po 3 kusech, važíme 1. a 2. skupinu, pak třeba 1. a 3.skupinu.
Z těchto 2 vážení vyplyne, ve které skupině je odlišná kulička a zda je to černá ovce (težší) nebo bílá vrána (lehčí).
1 < 2 a 1 < 3 v 1 skup. (BV)
1 > 2 a 1 > 3 v 1 skup. (CO)
1 > 2 a 1 = 3 v 2 skup. (BV)
1 < 2 a 1 = 3 v 2 skup. (CO)
1 = 2 a 1 > 3 v 3 skup. (BV)
1 = 2 a 1 < 3 v 3 skup. (CO)
Spotřebovali jsme tedy 2 vážení. Dále vezmeme 2 kuličky ze skupiny vybrané výše a zvážíme. Pokud váží stejně, zbývající je ta, co hledáme, v opačném případě je ta lehčí bílou vránou nebo ta těžší černou ovcí, což víme z prvních dvou vážení.
ÚLOHA číslo 15: (květen 2001)
Jarní sluníčko vylákalo na procházku do přírody maminku, taínka, jejich dvě děti a psa. Najednou došli k řece, přes kterou nebyl most, ani lávka. Naštěstí byla u břehu uvázaná loďka. Nosnost loďky je však jen 80kg. Maminka (M) váží 80 kg, tatínek (T) váží také 80 kg a každé dítě (D) váží 40 kg. Navíc sebou ještě mají psa (P), který váží 10kg. Psa musí stále někdo hlídat, aby se nezaběhl. Jak se dostanou na druhou stranu ? (Prázdná loďka jet nemůže, samotný pes také ne).
Řešení je více, vybíráme mail pana Pavla Surého:
|
Častá námitka byla o nepohodlnosti takové přepravy. Za všechny od pana Miroslava Beneše:
|
ÚLOHA číslo 14: (duben 2001)
Loď vyjede ráno z říčního přístavu A směrem do 250km vzdáleného přístavu B. Za celý den ujede 75 km. Protože v přístavu A je dobrá krčma, lodníci tajně v noci změní chod stroje a loď jede pozpátku, takže se vrátí o 50km zpět. Ráno ovšem kapitán vše pozná a loď se opět rozjede k přístavu B. Tak se to děje každý den a noc, přes den jede loď 75km dopředu, v noci 50km nazpět. Za jak dlouho bude v přístavu B?
Na úlohu se nachytalo jen několik řešitelů, většina odpověd byla správná, loď bude v přístavu 8. dne večer. Vybíráme řešení pana Pavla Kalety:
Cesta lodě bude trvat 8 dní. Můžeme na to přijít tak, že si budeme počítat kolik urazí každý den, nebo z rovnice:
n*d-(n-1)*z=/AB/, kde
d - vzdálenost, kterou urazí dopředu
z - vzdálenost, kterou urazí dozadu
n - počet dnů plavby
/AB/ - vzdálenost plavby
Předpokládá se, že když dorazí loď do přístavu, tak už je kapitán zpětnepustí...
ÚLOHA číslo 13: (březen 2001)
Král měl tři dcery: Anežku, Bertu a Cecílii.
Anežka vždycky mluvila pravdu, Berta vždycky lhala a Cecílie někdy mluvila pravdu a někdy lhala.
Ke dvoru přijel cizí princ, aby se ucházel o pravodomluvnou Anežku. Král jej zavedl do trůnní síně, kde všechny tři dcery seděly vedle sebe, a že princi Anežku dá, pokud pozná, která z nich to je. Přitom smí každé z nich položit jedinou otázku.
Princ chvíli přemýšlel a pak položil všem tutéž otázku:
"Jak se jmenuje princezna, která sedí uprostřed ?"
Princezna sedící vlevo odpoveděla: "Anežka."
Princezna sedící uprostřed odpověděla: "Berta."
Princezna sedící vpravo řekla "Cecílie."
Která z princezen je pravdomluvná Anežka?
Správných řešení přišlo mnoho, vybíráme úvahu pana Oldřicha Šošolíka:
Odpověď zní jednoznačně: Pravdomluvná Anežka sedí vpravo.
Zdůvodnění:
Seděla-li by Anežka vlevo, pak by nemohla její odpověď znít: "Anežka", protože by lhala. Pak tedy přicházejí v úvahu možnosti: 1. Anežka sedí uprostřed 2. nebo vpravo. Seděla-li by Anežka uprostřed, nemohla by její odpověď znít "Berta", protože by opět lhala. Z této úvahy vyplývá pouze jedna možnost, a to, že princezna Anežka sedí vpravo, uprostřed sedí princezna Cecílie a konečně vlevo sedí princezna Berta.
ÚLOHA číslo 12: (únor 2001)
V krabici s otvorem, do které nevidíte, je 7 červených kuliček, 15 modrých a 27 zelených. Kolik kuliček musíte minimálně vzít, abyste měli jistotu, že máte alespoň 2 kuličky stejné barvy?
K řešení lze dospět jednoduchou úvahou:
situace, že budu mít minimálně dvě stejně barevné kuličky nastane, když vytáhnu 4. Že se to dá spočítat i matematicky, předvedla - jako jediná - slečna (paní) Hana Zusková:
Chceme-li úlohu řešit matematicky, není to již tak snadné. Musíme počítat pravděpodobnosti pro 1, 2, 3, 4, atd. tahy, dokud nevyjde pravděpodobnost 100%, tedy pravděpodobnost jistého jevu.
Několik slov úvodem: Pravděpodobnost jevu A se nazývá číslo P(A)=m/n, kde n je počet všech možných výsledků náhodného pokusu a m je počet výsledků příznivých jevu A (tj. výsledků, při nichž nastává jev A). Pro pravděpodobnost sjednocení jevů A, B platí P(A u B) = P(A) + P(B) - P(A a B).
Pravděpodobnosti pro různý počet tahů:
1. Pravděpodobnost, že vytáhnu dvě kuličky stejné barvy, když tahám jen jednu je nulová, tady
P = 0/(7+15+27) = 0/49 = 0% - nevyhovuje
2. Pravděpodobnost, že vytáhnu minimálně dvě kuličky stejné barvy, když tahám dvě se dělí na tři části. Pravděpodobnost, že vytáhnu buď 2 červené nebo 2 modré nebo 2 zelené. Zde použijeme větu o sjednocení jevů A a B:
P = (7/49*6/48) + (15/49*14/48) + (27/49*26/48) = 40.5 % - také nevyhovuje
3. Pravděpodobnost, že vytáhnu minimálně dvě kuličky stejné barvy, když tahám tři se dělí na dvě části. Musíme spočítat pravděpodobnost, že vytáhnu všechny 3 stejné a pravděpodobnost, že vytáhnu 2 od stejné barvy a jednu od jiné. Takže:
P = (7/49*6/48*5/47) + (15/49*14/48*13/4 + (27/49*26/48*25/47) + (7/49*6/48*42/47)*3 +
+ (15/49*14/48*34/47)*3 + (27/49*26/48*22/47)*3 = 84.6 % - lepší, ale také nevyhovuje
Pozn.: Násobení 3 řeší posloupnost tahání (AAX, AXA, XAA).
4. Pravděpodobnost, že vytáhnu minimálně dvě kuličky stejné barvy, když tahám čtyři se dělí na čtyři části. Pravděpodobnost že vytáhnu všechny 4 stejné, 3 stejné, 2 stejné a musím ošetřit případ, kdy boudou 2 a 2 stejné (viz konec věty o sjednocení jevů A a B).
P = (7/49*6/48*5/47*4/46) + (15/49*14/48*13/47*12/46) + (27/49*26/48*25/47*24/46) +
+ (7/49*6/48*5/47*42/46)*4 + (15/49*14/48*13/47*34/46)*4 + (27/49*26/48*25/47*22/46)*4 +
(7/49*6/48*42/47*41/46)*6 + (15/49*14/48*34/47*33/46)*6 + (27/49*26/48*22/47*21/46)*6 -
- (7/49*6/48*15/47*14/46)*6 - (7/49*6/48*27/47*26/46)*6 - (15/49*14/48*27/47*26/46)*6 = 100 %
- to je ono!
Takže výsledkem je, že nám stačí 4 tahy, abychom měli jistotu, že máme alespoň 2 kuličky stejné barvy.
Výsledky jsou ověřeny simulačním programem, který provádí náhodné výběry.
ÚLOHA číslo 11: (leden 2001) - opět ze sbírky pana Pavla Havajíka
Zrcadlo, jak ho známe z každodenního života, prohazuje vlevo a vpravo. Jak je potom ale možné, že neprohazuje také nahoře a dole?! A dále: jak je možné, že tato vlastnost zrcadla zůstane zachována, když ho otočime o 90 stupňů?
Řešení od pana Miroslava Štefáníka: Zrcadlo vůbec strany neprohazuje, proto ho mohu otáčet třeba o 90 stupňů a obraz v zrcadle vypadá pořád stejně. Problém je podle mne pouze v tom, že pojem vpravo a vlevo je pouze relativní. Záleží, z které strany se na věc díváme. Pokud stojíme s někým proti sobě tváří v tvář, pak to, co já mám po levé ruce má můj protivník po pravé a naopak. V zrcadle mi pak mého protivníka nahrazuje můj vlastní obraz. Pěšinka na mém účesu je tedy stále na stejné straně - vlevo (i v zrcadle), ale z pohledu mého vlastního zrcadlového obrazu je vpravo.
ÚLOHA číslo 10: (prosinec 2000) - velmi pěknou úlohu zaslal pan Pavel Havajík
Jak v prakticky libovolném assembleru zjistit, zda je číslo mocnina 2? Praktická úloha, hodí se například při zjištěni platného stisku tlačítek - výsledek udává, že je nastaven právě 1 bit z bytu (slova). Při řešeni nesmíte použít cyklus. Jsou dovoleny přesuny, aritmetické a logické operace.
Úloha není určena jen programátorům, stačí popsat princip výpočtu slovně.
Tato úloha byla tvrdým oříškem. Výsledek je ale překvapivě jednoduchý (číslo předpokládáme v registru A): Spočítáme
A AND (A-1) a výsledek testujeme na nulovost.
Logické zdůvodnění poslal pan ing. Zdeňek Skalák: pokud předpokládáme, že dané číslo je mocninou dvou, tj. má ve svém binárním vyjádření pravě jednu "1", dá se zapsat jako: n*01m*0 (tj: n nul, 1, m nul). Pro obecné číslo platí, že se dá zapsat jako n*x1m*0, (tj. n 0 nebo 1, 1, a m 0 - s výjimkou čísla 0). Odečtu-li od tohoto čísla číslo jedna, dostanu číslo n*x0m*1 (tj. všechny samé 0 zprava se změní na 1, nejpravější 1 na 0 a vše vlevo zůstane). Pokud pro toto číslo provedu operaci AND (logický součin) s původním číslem, dostanu číslo (n*x1m*0 AND n*x0m*1 = n*x0m*0). Toto výsledné číslo se rovna číslu 0 právě pokud mělo původní číslo n*x rovno n*0, tj. pokud původní číslo mělo ve svém binárním vyjádření právě jednu 1. Jak jsem v úvodu vzpomenul, je výjimkou číslo 0, proto zvlášť: 0 = m*0 0-1= m*1 m*0 AND m*1 -> m*0, tudíž pro nulu toto platí taky.
ÚLOHA číslo 9: (listopad 2000)
Cyklista vyjede z Prahy. Když přijede do Kolína, vyjede za ním z Prahy automobil, který jede mnohem rychleji. V okamžiku, kdy je automobil v Kolíně, je cyklista už o pěkný kus dále, v Kutné Hoře. Automobil tedy pokračuje. V okamžiku, kdy dojede do Kutné Hory, je cyklista už opět dále. Takže vždy když auto přijede na místo, kde byl před chvílí cyklista, už je cyklista zase o kousek dále. Tato situace se samozřejmě stále opakuje, takže to tedy znamená, že ho auto bude stále honit a nikdy nedohoní. Kde je v této úvaze chyba?
Úloha je slovně modifikovaná, pochází ze starého Řecka (Achilles a želva). Řešení je námětem k diskuzi (i my jsme se v naší firmě trochu pohádali). Proto jsme také do slosování zařadili všechny, kdo se zúčastnili. Pěkně vše popsal (logicky i matematicky) pan Luděk Beran:
V úvaze se chybně předpokládá, že auto nikdy nemůže dostihnout cyklistu, protože by muselo za konečný čas překonat nekonečně mnoho úseků. To však možné je, neboť součet nekonečného počtu těchto úseků dává konečnou vzdálenost (konvergentní geometrická řada).
Toto můžeme dokumentovat na příkladu:
Pro jednoduchost předpokládáme, že rychlost auta je 2 x vyšší než rychlost cyklisty a náskok cyklisty je 1. Až se dostane auto na místo, odkud vyjel cyklista, získá cyklista náskok 1/2. Když se na toto místo dostane auto, cyklista bude mít náskok 1/4 atd. Náskok cyklisty se tedy zmenšuje geometrickou řadou s quocientem q = 1/2. Protože tato řada je konvergentní, dostane se auto na úroveň cyklisty po projetí konečné vzdálenosti s = 1 + 1/2 + 1/4 + 1/16 ...... = 2(součet nekonečné řady s = a1/(1-q) = 1/(1-1/2) = 2), kterou překoná za čas t = s/v (v - rychlost auta).
ÚLOHA číslo 8: (říjen 2000)
Nepoctivý sklepmistr nalezl 10 litrový plný sud vína. Natočil si džbánek a vypil ho, a aby nikdo nic nepoznal, dolil sud vodou. Druhý den, když se vše v sudu promíchalo, sklepmistr natočil opět plný džbánek a sud zase dolil vodou. A tak se stalo, že víno bylo ředěno právě 1:1. Jaký objem měl sklepmistrův džbánek?
Správné řešení zaslal například pan Milan Křapáček. Někteří účastníci řešili úlohu bez kvadratické rovnice - úvahou
Když mělo být víno zředěno 1:1, muselo v sudu zůstal 5 litrů vína a stejné množství vody. Objem sklepmistrova džbánku označím proměnou x.
První den:
Sklepmistr si nalil víno o objemu x, to znamená, že v sudu zůstalo (10-x) litrů vína a x (původní víno bylo "čisté", to znamená, že neobsahovalo vodu).
Druhý den:
Sklepmistr si nalil další džbánek vína, ale protože bylo dobře promícháno, tak si mimo vína nalil i něco málo vody. Kolik vína a kolik vody si nalil záleží na poměru vína a vody po prvním dnu. Dostáváme kvadratickou rovnici:
(10-x)-x*(10-x)/10=5
Číslovka pět je obsah vína ve zředění 1:1 tedy 5 litrů.
Dostáváme 2 řešení, ale jen jedno je vyhovuje. x = 10-5*sqrt(2)=2,9289 litru.
(sqrt je druhá odmocnina.)
ÚLOHA číslo 7: (září 2000)
V uvedeném nápisu je každá číslice zakódována jedním písmenem. Nahraďte písmena číslicemi tak, aby výpočet byl správný. (+ není číslice, ale znak součtu)
MARIE
+IVO
+IVO
-------
RUPIE
Dvě správná řešení zaslal například pan Pavel Havajík. Existují 2 kombinace, dávající správný výsledek:
69782
+850
+850
-------
71482
69783
+850
+850
-------
71483
ÚLOHA číslo 6: (srpen 2000)
Kolega přinesl do práce černou skřínku se dvěma svorkami označenými 220V. Zapojili jsme jí do zásuvky a do série jsme dali střídavý ampérmetr. Pro jistotu jsme ještě měřili napětí přímo na svorkách krabičky střídavým voltmetrem. Voltmetr ukázal 230V a ampérmetr 1A (přístroje jsou v pořádku). Přesto se černá skřínka ani trochu nezahřála a taky elektroměr se ani nehnul. Jak to vysvětlit? Co by v této skřínce mohlo být?
Správné řešení poslal například pan Rostislav Pelc:
V černé skříňce je zařízení, u kterého je fázový posun napětí a proudu roven hodnotě +Pí/2 nebo -Pí/2 (např. ideální kapacita nebo indukčnost). Potom střídavý ampérmetr měří efektivní hodnotu jalového proudu. Činný výkon P=0, jalový výkon přelévá energii navzájem mezi zdrojem a spotřebičem (vytváří elektrostatické resp. magnetické pole). Celkový výkon je tedy roven nule - elektroměr neukazuje spotřebu.
A jak spočítali jiní řešitelé, pokud je v černé skřínce kondenzátor, pak jeho kapacita je 13.8 mikrofaradů.
ÚLOHA číslo 5: (červenec 2000)
Čtyři muži chtějí přejít most. Všichni začínají na jedné straně. Je noc a oni mají pouze jednu baterku. Najednou můžou most přejít pouze dva a každá skupinka (ať jednočlenná nebo dvoučlenná) musí mít baterku s sebou. S baterkou se vždy musí někdo vrátit (tzn. nemůže se přehodit přes most atd.). Každý muž chodí jinak rychle. Dvojice musí jít rychlostí toho pomalejšího. První muž potřebuje k přechodu mostu 1 minutu, druhý 2 minuty, třetí 5 minut a čtvrtý 10 minut. Např.: když první a třetí muž přecházejí most spolu, trvá jim to 5 minut.
Jakým způsobem mohou přejít most všichni čtyři za17 minut?
Názorné grafické řešení úlohy zaslal pan ing. Ladislav Mitter:
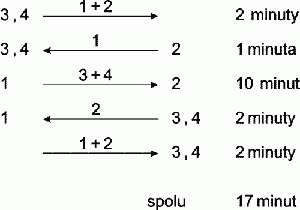
ÚLOHA číslo 4: (červen 2000)
Pan Josef Chytrý přijel k babičce na chalupu. V kuchyni se jí spálila žárovka a protože jí nedávno předělali napětí ze 110V na 230V, neměla novou. Pan Chytrý si však věděl rady. Nalezl v kapse diodu, vložil ji do série s žárovkou určenou pro 110V a bylo to. Udělal to správně?
Správné řešení od ing. Milana Kučery:
Pan Chytrý to správně neudělal. Je třeba určit efektivní hodnotu napětí, které je jednocestně usměrněné. Hodnotu efektivního napětí získáme podílem integrálu funkce sin^2(t) od nuly do Pí v čitateli a hodnoty 2*Pí ve jmenovateli. Výpočtem vyjde hodnota Uef =0.5 Umax. Maximální hodnota napětí 230V je 325.2V, efektivní hodnota jednocestně usměrněného napětí je pak 162.6V. Použitá žárovka je na110V a tak nevydrží.
Logickou úvahou (od stejného autora):
žárovka na 110V by na síti 220V svítila 4x větším výkonem, pokud ji však polovinu půlvln odpojíme (diodou), bude svítit jen 2x větším výkonem. Efektivní napětí na ní tedy bude o odmocninu ze dvou větší než při správném napájení.
ÚLOHA číslo 3: (květen 2000)
Jednoho dne přišel Honza ke králi, který měl tři dcery. Rozhodl se, že si jednu vezme za ženu. Král mu slíbil, že si může vybrat, kterou chce, když uhádne věk každé z nich, a pravil mu: "Podívej se na můj les. Když napíšeš počet stromů dvakrát vedle sebe, dostaneš šestimístné číslo. Když to číslo počtem stromů vydělíš, dostaneš součin věku mých 3 dcer. A to ti musi stačit."b>
Správné řešení například od pana Miroslava Beneše:
Pokud budeme uvažovat libovolné trojmístné číslo ABC, pak dvě tato čísla napsaná vedle sebe budou ve tvaru ABCABC a po vydělení původním číslem dostaneme číslo 1001. Toto má být součinem věku tří dcer. Jediné možné rozložení na tři činitele je 1001 = 13 x 11 x 7. Proto věk tří dcer je 7, 11 a 13 let..
ÚLOHA číslo 2: (duben 2000)
Je určena pro programátory procesoru typu 8051 - nepřímé adresování bitu. V registru A je číslo 0 až 7. Napište proceduru, která v proměnné X nastaví bit číslo A podle stavu C (carry). Proměnná X může být umístěna v bitově adresovatelné oblasti.
Přišlo hodně shodných řešení. Protože kritériem byla rychlost provádění, vylosovali jsme z řešitelů, kteří použili proceduru s tabulkou. Vítězem se stal pan ing. Jiri Engelthaler. Podívejte se na řešení s tabulkou i bez.
| SET: mov DPTR,#TAB movc A, @A+DPTR jnc SET1 orl X, A sjmp SET2 SET1: cpl A anl X, a SET2: ........ TAB: DB 01h,02h,04h,08h,10h,20h,40h,80h |
SET: inc A mov R0,A mov A,#80H LOOP: rl A djnz R0,LOOP vjnc SET1 orl X,A sjmp SET2 SET1: cpl A anl X,A SET2: ...... |
ÚLOHA číslo 1: (březen 2000)
Stanovte odpor, který naměříme na svorkách zapojení podle obrázku. V zapojení je použito nekonečně mnoho rezistorů stejné hodnoty R.
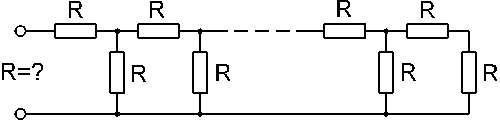
Správný postup řešení od pana Petra Lupínka:
Jelikož se jedná o nekonečný řetězec, pak se nic nestane, když odebereme první dvojici rezistorů. Je-li hledaný odpor soustavy X, pak se jedná o paralelní kombinaci R spolu s odporovou řadou X a přičteme ještě R.
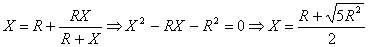
Výsledný odpor je tedy 1,618 R
K výsledku poslal velmi zajímavý komentář pan ing. Jiří Šindýlek:
Po vyčíslení vzorce je výsledná konstanta Fi=X/R=(1+Sqr(5))/2. Víte, že se jedná o konstantu Zlatého řezu (Golden ratio?)

